微服务-02-一致性Hash

Microservices Comments

问题背景

以缓存为例，在整个微服务系统中，缓存可以是多个节点

  • 一是为了提高稳定，单节点宕机情况下，整个存储就面临服务不可用
  • 二是数据容错，同样单节点数据物理损毁，而多节点情况下，节点有备份，除非互为备份的节点同时损毁

为了更好的访问各个节点，使用了Hash算法。把任意长度的输入通过散列算法变换成固定长度的输出，该输出就是散列值，对应不同的节点。如果直接使用取模的方式，如：

value=key%Nvalue = key \% N

其中N为缓存节点(访问单元)的数目，当节点因为异常而退出的时候

  • 如果未感知N的变化，那么单个节点所有key都无效导致无法访问，容易引起缓存雪崩
  • 如果感知到N的变化 N = N - 1，那么整个集群所有的 Key 都移位，更加容易引起缓存雪崩
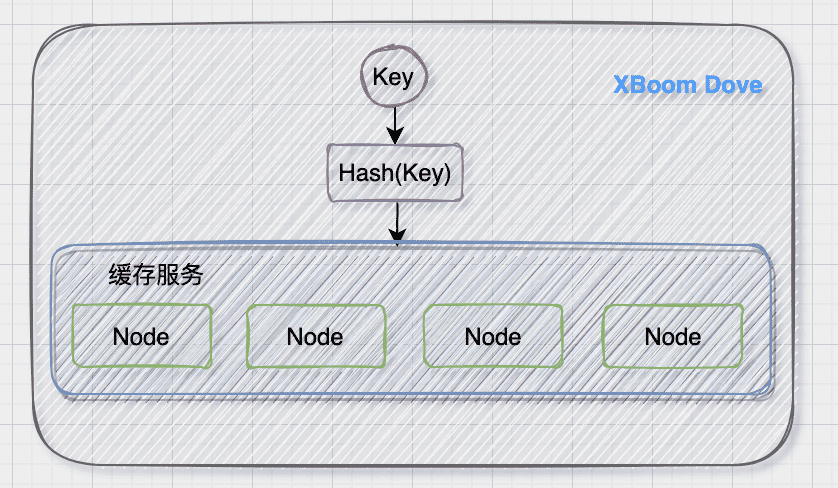
micro-cache-5

所以就引入了一致性Hash(Consistent Hash)

实现原理

基础类型

最基础的一致性 hash 算法就是把节点直接分布到环上，从而划分出值域， key 经过 hash(key) 之后，落到不同的值域，则由对应的节点处理(图中逆时针)

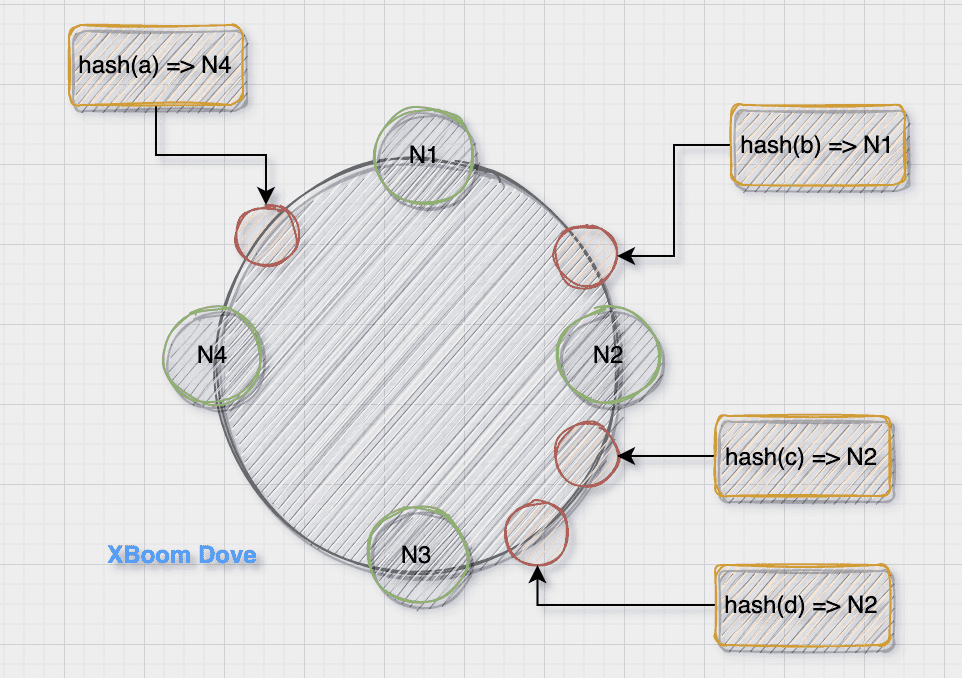
micro-cache-6
新增节点

当在N2节点与N3节点之间新增N5节点的时候，只有d的位置受到了影响，其他不变

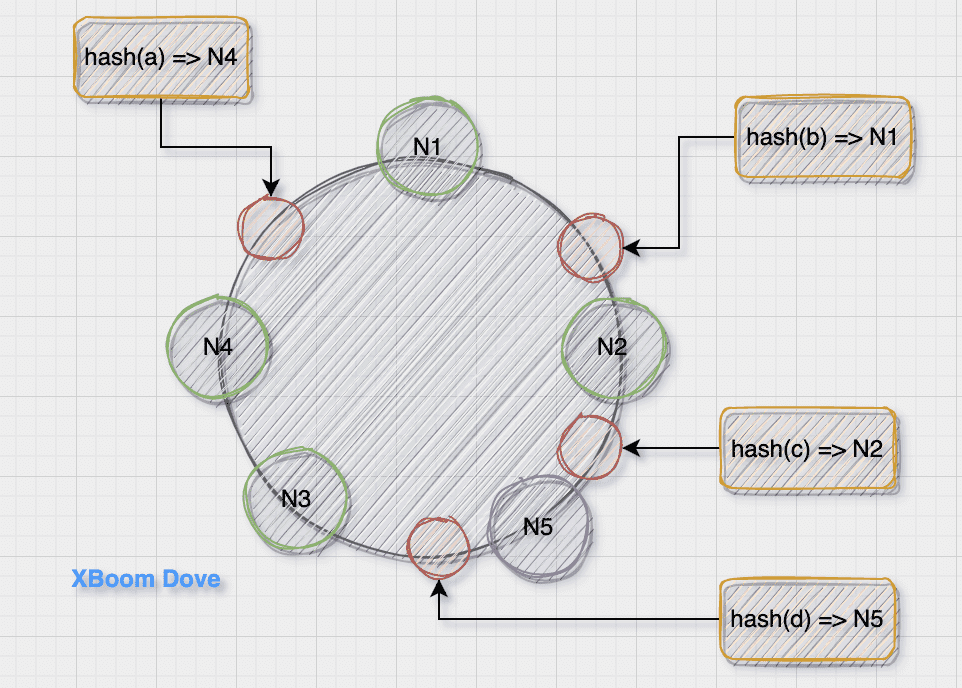
micro-cache-7
删除节点

当删除N2节点的时候，也只有c的位置收到的影响

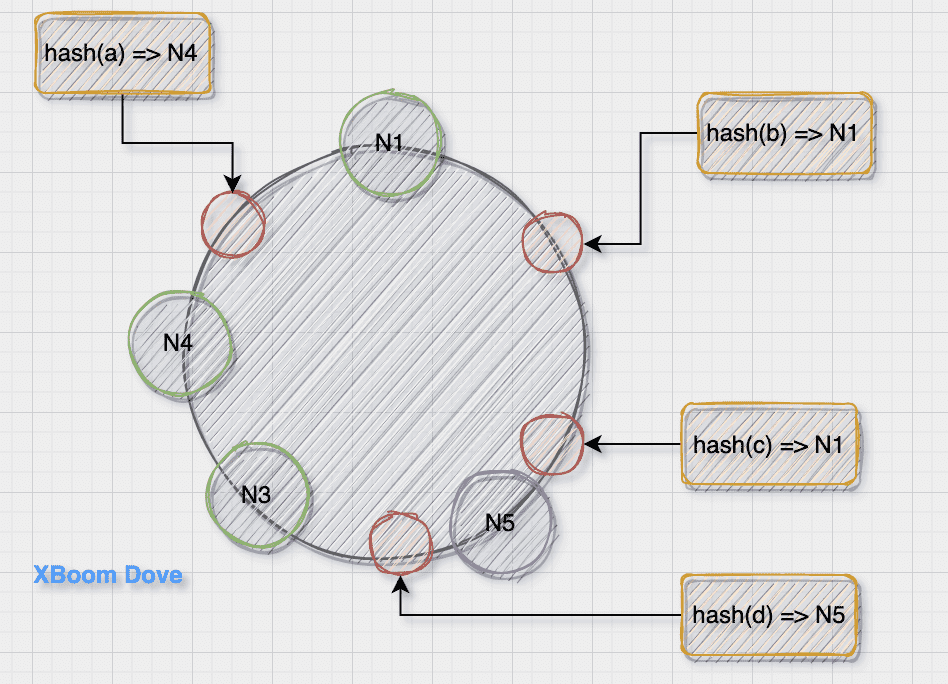
micro-cache-8

这样仍然存在问题：

  1. 随机分布节点的方式使得很难均匀的分布哈希值域(物理节点较少)

  2. 在动态增加节点后，即使原来是均匀分布后面也不再均匀分布；

  3. 增删节点带来的一个较为严重的缺点是：

    • 当一个节点异常时，该节点的压力全部转移到相邻的一个节点；

    • 当一个新节点加入时只能为一个相邻节点分摊压力；

虚拟节点

针对基础一致性 hash 的缺点一种改进算法是引入虚节点(virtual node)的概念。这个本质的改动：值域不再由物理节点划分，而是由固定的虚拟节点划分，这样值域的不均衡就不存在了。

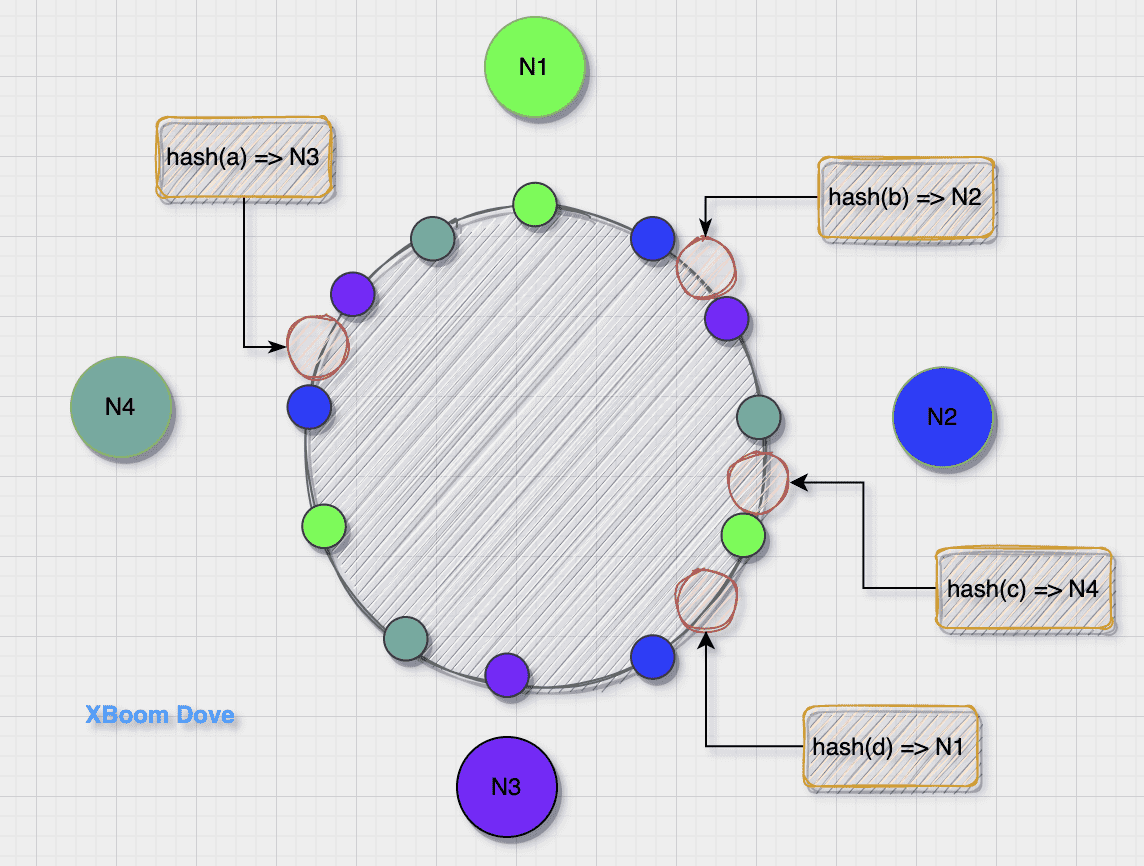
micro-cache-9

注意：

  1. 虚拟节点的个数要远大于物理节点的个数
  2. 虚拟节点的分布是交错的，如果只是虚拟节点增加而不交叉，会无法在删除/新增节点时分摊压力
  3. 每个物理节点对应的虚拟节点也是相等的，可以使节点平均分配
  4. 操作数据时，首先通过数据的哈希值在环上找到对应的虚节点，进而查找元数据找到对应的真实节点（旁白：所以这部分元数据是需要存下来的);

那么这个时候再来删除和新增节点的时候，就能很好的分摊压力了

  • 增节点的时候要能为多个节点分摊压力
  • 删节点的时候要能让多个节点承担压力
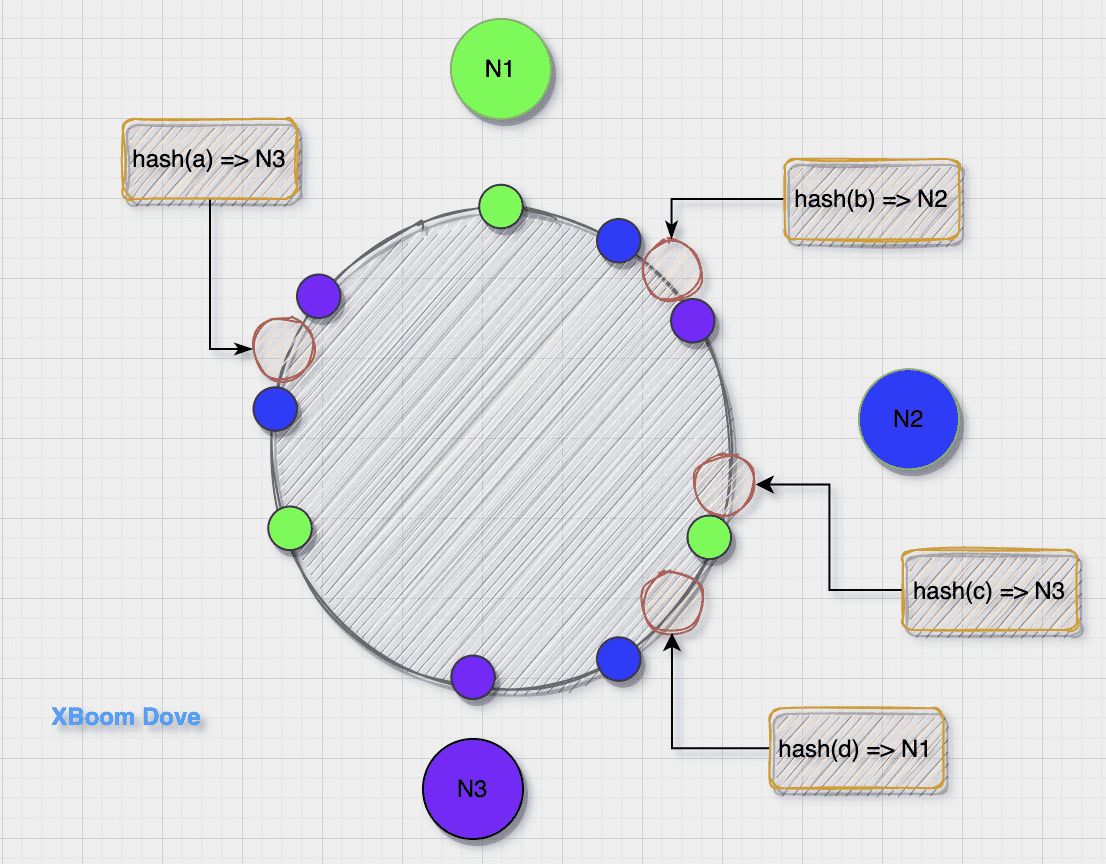
micro-cache-10

存在的问题

  1. 如何通过Key的Hash值找到对应范围所属的节点

    认为Hash计算的值是随机的，符合概率分布。计算完所有节点的Hash之后需要进行一个排序

  2. 排序完怎么做到虚拟节点的交叉

    通过计算每个虚拟节点的Hash值，然后整体进行排序

技术内幕

这里看看go-zero是如何实现一致性Hash的

对象定义

根据原理可知，实现一个一致性Hash需要知道

  1. 物理节点对应的虚拟节点的数目
  2. Hash函数
  3. 物理节点与虚拟节点的对应关系
  4. 环中虚拟节点的排序
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
const (
	TopWeight = 100   //权重

  minReplicas = 100	//虚拟节点:物理节点
	prime       = 16777619  //名称前缀
)

type (
	// Func defines the hash method.
	Func func(data []byte) uint64

	// A ConsistentHash is a ring hash implementation.
	ConsistentHash struct {
		hashFunc Func	//Hash函数
		replicas int	//虚拟节点的数量
		keys     []uint64	//保存虚拟节点的Hash
		ring     map[uint64][]interface{}					//存储虚拟节点与物理节点的关系 
		nodes    map[string]lang.PlaceholderType	//存储节点的信息
		lock     sync.RWMutex
	}
)

// 可以理解为确定node字符串值的序列化方法
// 在遇到哈希冲突时需要重新对key进行哈希计算
// 为了减少冲突的概率前面追加了一个质数prime来减小冲突的概率
func innerRepr(v interface{}) string {
   return fmt.Sprintf("%d:%v", prime, v)
}

// 可以理解为确定node字符串值的序列化方法
func repr(node interface{}) string {
   return mapping.Repr(node)
}

新增节点

增加节点副本数
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
func (h *ConsistentHash) AddWithReplicas(node interface{}, replicas int) {
	h.Remove(node)	//如果同名则先删除

	if replicas > h.replicas {	//虚拟节点数量不能超过一致性Hash数量
		replicas = h.replicas
	}

	nodeRepr := repr(node)	//找到节点表达式
	h.lock.Lock()
	defer h.lock.Unlock()
	h.addNode(nodeRepr)			//添加添加

  //添加虚拟节点
	for i := 0; i < replicas; i++ {
		hash := h.hashFunc([]byte(nodeRepr + strconv.Itoa(i)))	//计算虚拟节点名称获取Hash值
		h.keys = append(h.keys, hash)							//保存虚拟节点
    h.ring[hash] = append(h.ring[hash], node)	//为虚拟节点添加物理节点
	}

	sort.Slice(h.keys, func(i, j int) bool {	//进行虚拟节点的排序
		return h.keys[i] < h.keys[j]
	})
}

func (h *ConsistentHash) addNode(nodeRepr string) {
	h.nodes[nodeRepr] = lang.Placeholder
}

注意：

  1. h.ring[hash]这里使用的是切片，为了防止虚拟节点存在冲突，也就是一个虚拟节点可能对应多个物理节点。
设置权重节点
1
2
3
4
5
6
7
// 按权重添加节点
// 通过权重来计算方法因子，最终控制虚拟节点的数量
// 权重越高，虚拟节点数量越多
func (h *ConsistentHash) AddWithWeight(node interface{}, weight int) {
    replicas := h.replicas * weight / TopWeight
    h.AddWithReplicas(node, replicas)
}

删除节点

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
func (h *ConsistentHash) Remove(node interface{}) {
	nodeRepr := repr(node)	//找到节点表达式

	h.lock.Lock()
	defer h.lock.Unlock()

  //如果不包含该节点直接退出
	if !h.containsNode(nodeRepr) {
		return
	}
  
	for i := 0; i < h.replicas; i++ {
		hash := h.hashFunc([]byte(nodeRepr + strconv.Itoa(i)))	//虚拟节点Hash值
		index := sort.Search(len(h.keys), func(i int) bool {	//查找虚拟节点
      return h.keys[i] >= hash //二分法进行节点查找
		})
		if index < len(h.keys) && h.keys[index] == hash {	//如果是要找的虚拟节点则删除这个虚拟节点
			h.keys = append(h.keys[:index], h.keys[index+1:]...)
		}
		h.removeRingNode(hash, nodeRepr) //删除虚拟节点对应物理节点
	}
  
  //删除物理节点
	h.removeNode(nodeRepr)
}

func (h *ConsistentHash) removeRingNode(hash uint64, nodeRepr string) {
	if nodes, ok := h.ring[hash]; ok {
		newNodes := nodes[:0]
		for _, x := range nodes {	//遍历物理节点
			if repr(x) != nodeRepr {	//如果物理节点与指定的不一样
				newNodes = append(newNodes, x) //就把节点存入新的节点中
			}
		}
    //虚拟节点存在多个物理节点则仅保留新的，否则直接删除虚拟节点
		if len(newNodes) > 0 {	
			h.ring[hash] = newNodes
		} else {
			delete(h.ring, hash)	
		}
	}
}

func (h *ConsistentHash) removeNode(nodeRepr string) {
	delete(h.nodes, nodeRepr)
}

注意：

  1. 使用二分法进行节点查找
  2. 由于一个虚拟节点对应多个物理节点，不能直接删除虚拟节点

获取节点

根据v顺时针找到最近的虚拟节点，再通过虚拟节点映射找到真实节点

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
func (h *ConsistentHash) Get(v interface{}) (interface{}, bool) {
	h.lock.RLock()
	defer h.lock.RUnlock()

	if len(h.ring) == 0 {
		return nil, false
	}

  // 二分查找
  // 找到比Hash的第一个节点，可能返回的 index = len(h.keys)
  // 所以这里取余回到第一个节点
	hash := h.hashFunc([]byte(repr(v)))	//Key的Hash值
	index := sort.Search(len(h.keys), func(i int) bool {
		return h.keys[i] >= hash
	}) % len(h.keys)

	nodes := h.ring[h.keys[index]]	//获取虚拟节点对应物理节点
	switch len(nodes) {
	case 0:
		return nil, false
	case 1:
		return nodes[0], true
	default: //存在Hash冲突
    // 取模的方式存获取真实物理节点
		innerIndex := h.hashFunc([]byte(innerRepr(v)))
		pos := int(innerIndex % uint64(len(nodes)))
		return nodes[pos], true
	}
}

注意:

  1. 如果虚拟节点对应多个物理节点那么通过hash获取在节点中的位置

总结

  1. 通过增加虚拟节点的数目来使的hash的分布更加均匀
  2. 虚拟节点的应该是交叉的(实现中并不是严格交叉，而是通过Hash再排序让虚拟节点交叉存在)

参考链接

  1. 分布式系统基石一
  2. 搞懂一致性Hash
  3. https://talkgo.org/t/topic/3098