八数码问题也称为九宫问题。在3×3的棋盘,摆有八个棋子,每个棋子上标有1至8的某一数字,不同棋子上标的数字不相同。棋盘上还有一个空格,与空格相邻的棋子可以移到空格中。要求解决的问题是:给出一个初始状态和一个目标状态,找出一种从初始转变成目标状态的移动棋子步数最少的移动步骤
所谓一个状态就是棋子在棋盘上的一种摆法。棋子移动后,状态就会发生改变。实际上就是找出从初始状态到达目标状态所经过的一系列中间过渡状态
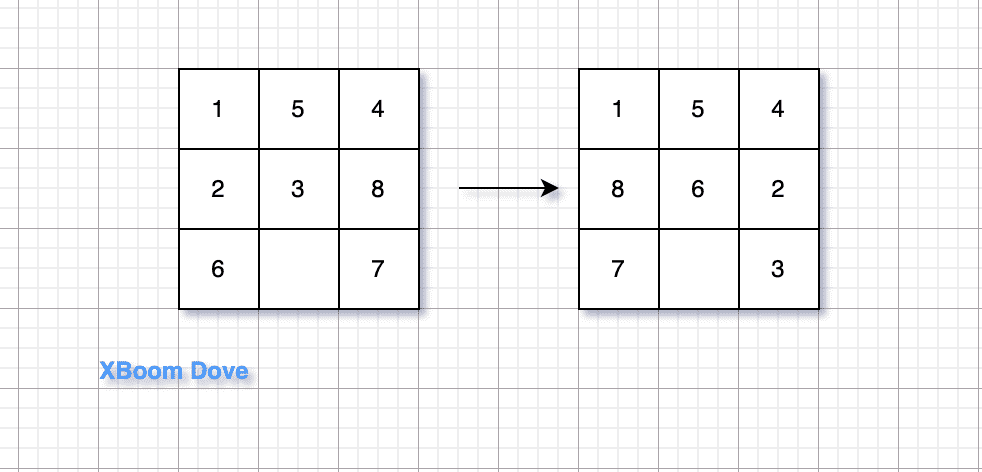
首先这个九宫格的状态数量是 9!,那么存在问题
-
是否存在从一个状态转移到另外一个状态无解的情况?
-
如何计算或者衡量从一个转移到另外一个状态的需要走多少步?
排列的性质
为了搞清楚上述问题,需要知道几个基本定义与引理
-
把n个不同的元素按一定的顺序排列成一行,成为这n个元素的一个排列。n个不同元素的排列共有 n! 种
-
对于n个自然数的一个排列,如果一个大数排在一个小数之前,就称这两个数构成一个逆序。一个排列的逆序总和称为该排列的逆序对,记为
如5阶排列31542的逆序是(3,1),(3,2),(5,4),(5,2),(4,2),故
-
逆序对为奇数的排列称为奇排列。逆序对为偶数的排列称为偶排列。自然排列 123⋯n的逆序对为0,故它是偶排列
-
在一个排列中,把某两个数的位置互换(其他数不动)变成另一个排列的变动称为一个对换,将相邻的两个数对换称为相邻对换
性质的证明
性质1:一个排列中的任意两个数对换后,排列改变奇偶性。即经过一次对换,奇排列变成偶排列,偶排列变成奇排列
证明:
-
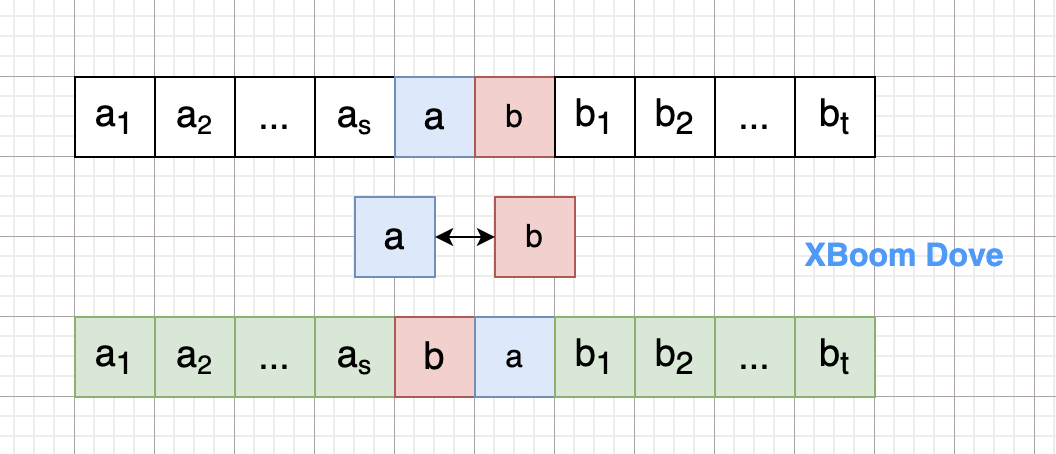
先证明相邻对换的情形
-
设排列 ,对换a 与 b 的排列变为
-
a 与 b 的 对换不影响 , 与 其他数的关系
-
但a与b的序关系变为:
-
当 a < b 时,在新排列中 a 、b 构成逆序
-
当 a > b 时,在新排列中 a、b 不构成逆序
-
-
因此 比 的逆序多1或者少1
-
-
再证一般对换情形
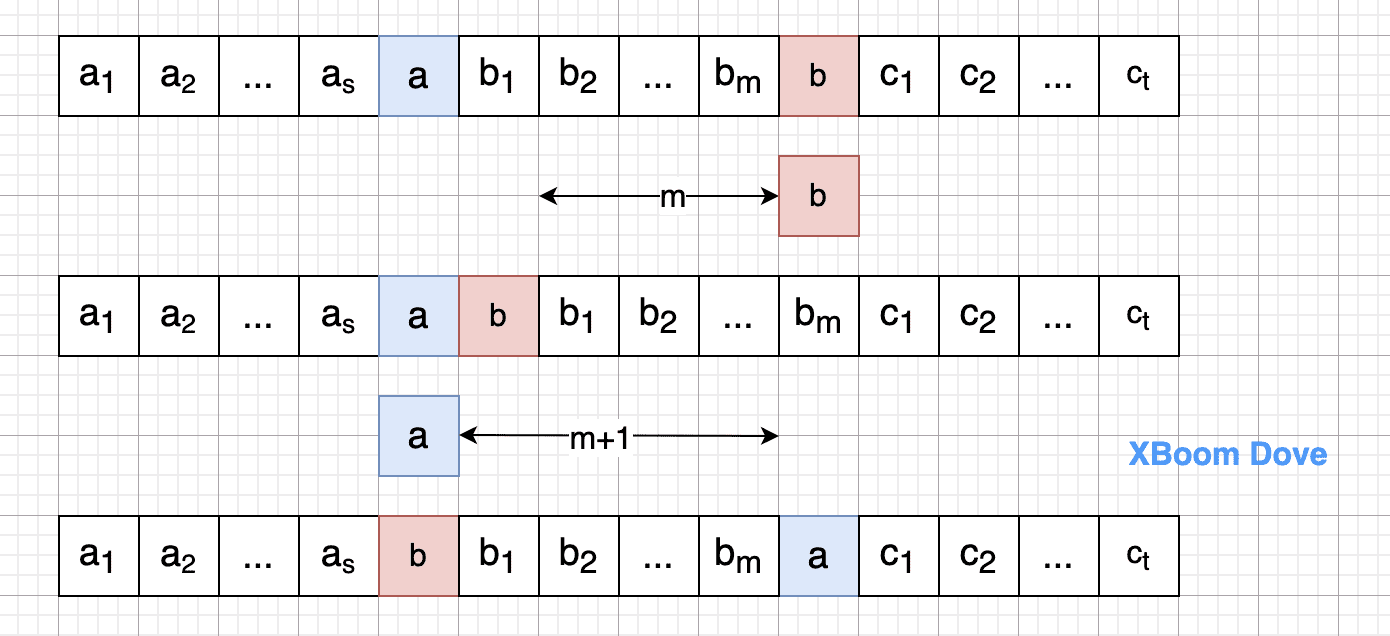
- 设存在排列
- 将 b 做 m 次相邻对换变为
- 再将 a 做 (m + 1) 次相邻对换变为
- 所以 经过 (2m + 1) 次相邻兑换,可以把排列 转变成,这两个排列的奇偶性相反
性质2:在全部的 n(n≥2)阶排列中,奇偶排列各占一半,各有 n!/2 个
证明:
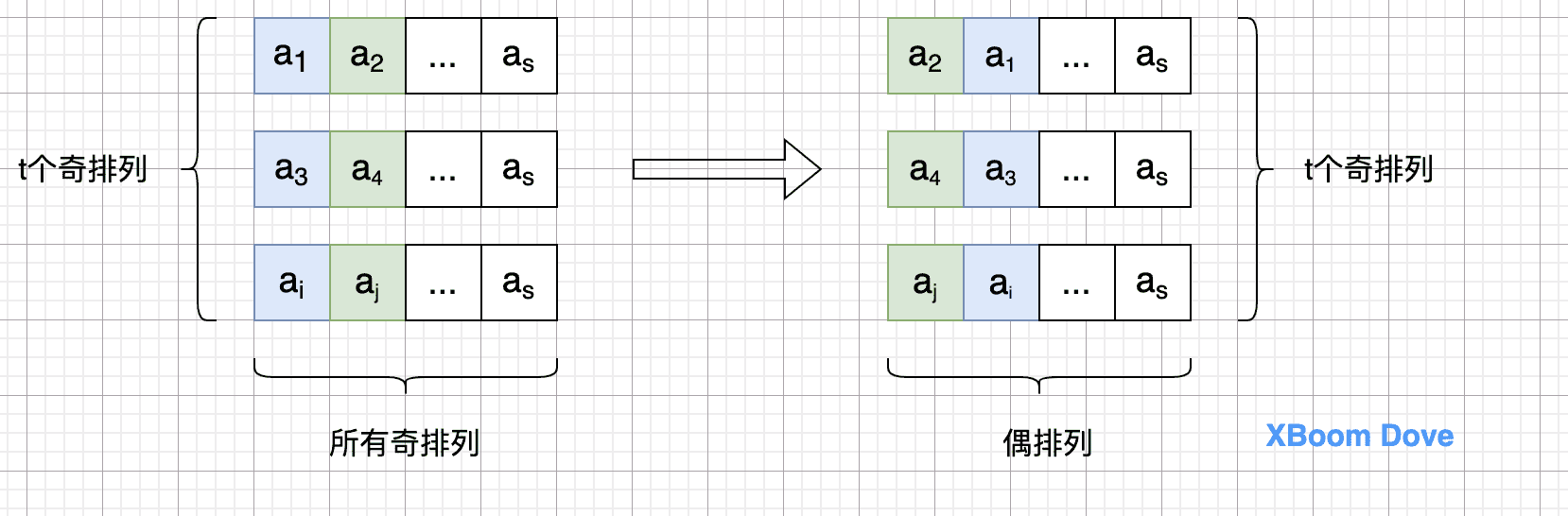
-
假设在全部n级排列中共有t个奇排列,s个偶排列
-
将t个奇排列中的前两个数字对换,得到t个互不相同的偶排列。因此 t≤s
-
同理可证 s≤t
-
于是 s=t,即奇、偶排列的总数相等,各有 n!/2个
性质3:任意一个n阶排列都可以经过一系列对换变成自然排列,并且所作对换的次数与这个排列有相同的奇偶性
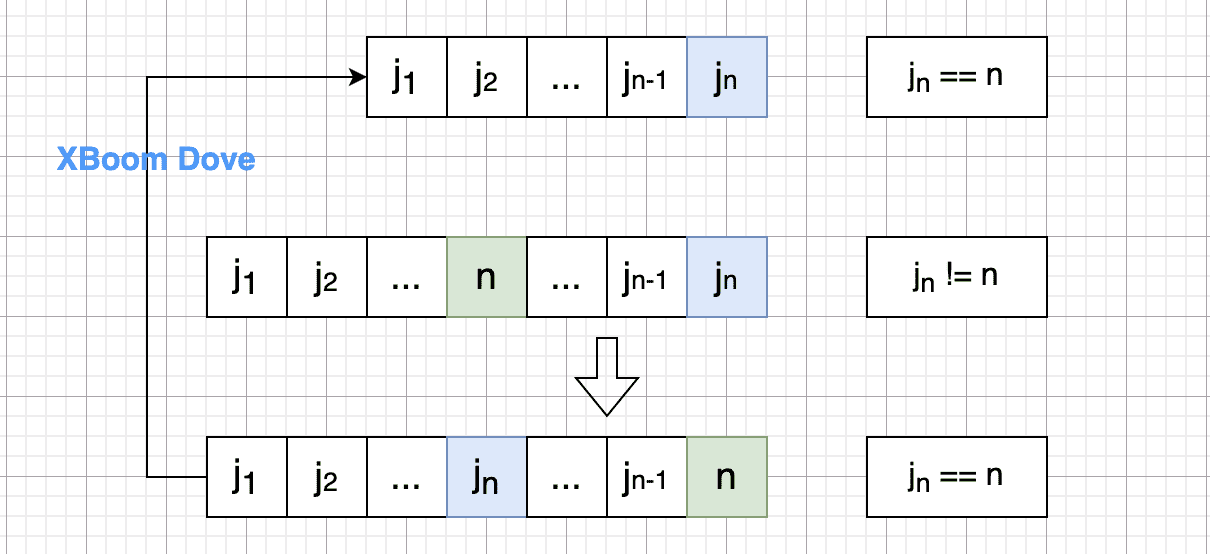
证明(归纳法):
- 1阶排列只有一个,结论显然成立
- 假设对n-1阶排列已经成立,证对n阶排列的情形结论也成立
- 设 是一个n阶排列
- 如果 ,假设n-1级排列 可以经过一系列变换变成自然序列,即 1 2 … n−1,于是这一系列对换也就把 j1j2⋯jn 变成 12⋯n 这种自然序列的形式。
- 如果 ,那么对 作 和 n 的对换,它就变成 ,这就归结成上面的情形,因此
- 设 是一个n阶排列
性质4:奇偶性与可达性关系与证明
必要性证明:排列的奇偶性不同则对应在八数码问题中不可达
在满足上述约定的八数码问题中,空格与相邻棋子的交换不会改变棋局中棋子数列的逆序对的奇偶性
-
空格与左右棋子交换:是不改变棋子数列的逆序对的(因为数列并没有改变)
-
空格与上下棋子交换:也是不改变棋子数列的逆序对的
- 假设交换棋子为c[i]=X
- 原数列p=c[1]… X c[i+1]c[i+2]…c[8]将变为新数列q=c[1]…c[i+1]c[i+2]X …c[8](注意:在棋盘中,上下相邻的两棋格之间隔有两个棋格)。可以解释为用X与c[i+1]、 c[i+2]先后进行两次相邻交换而完成状态转变。
- 由p状态到q状态并不会改变改变棋子数列的逆序对的奇偶性。同理可证空格与下方棋子交换也不会改变棋子数列的逆序对的奇偶性。所以,空格与相邻棋子的交换不会改变棋局中棋子数列的逆序对的奇偶性
得出 定理1:对于任意两个状态映射的序列,如果这两个状态等价,那么它们的逆序数相同
充分性证明:排列的奇偶性相同则对应在八数码问题中也可达
首先明确几个定义:
-
状态(state):八数码中8个数字与0的排列被定义为八数码的状态,比如:
-
状态空间(state space):八数码所有状态的合集被称为状态空间
-
完全态(completeness):当状态空间的子集中任何两个状态都能通过一定步骤得到,那么称这个状态空间的子集是完全态
-
状态映射(a sequence mapped by a state):一个状态{}可以映射(忽略0)成一个排序,那么这个排列就称为这个状态的映射
-
标准格式(a standard form):如果 0 在正中间,那么称这个状态为标准格式

-
区域(field):对于任意状态(state),4个位置中任意两个都相邻,那么称之为 区域,特别的,当两个区域有相同的两个位置,则称为 同边区域
-
转圈(circle moving):0在一个区域内移动称 转圈
引理1:对于标准格式中的任意区域,转圈可以得到两个等价的区域
考虑到 标准格式 的对称性,只需要考虑一个区域的的变化
第一种情况(顺时针方向部分先后): a b d
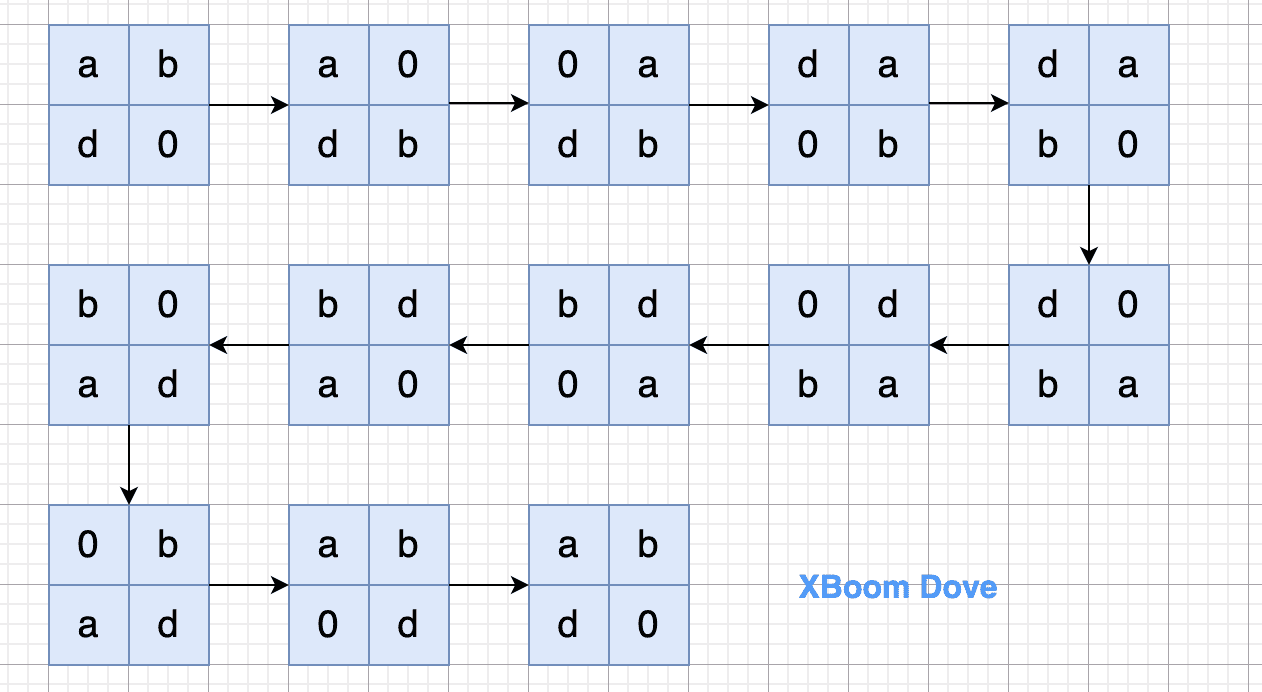
第二种情况(顺时针方向不分先后): a d b
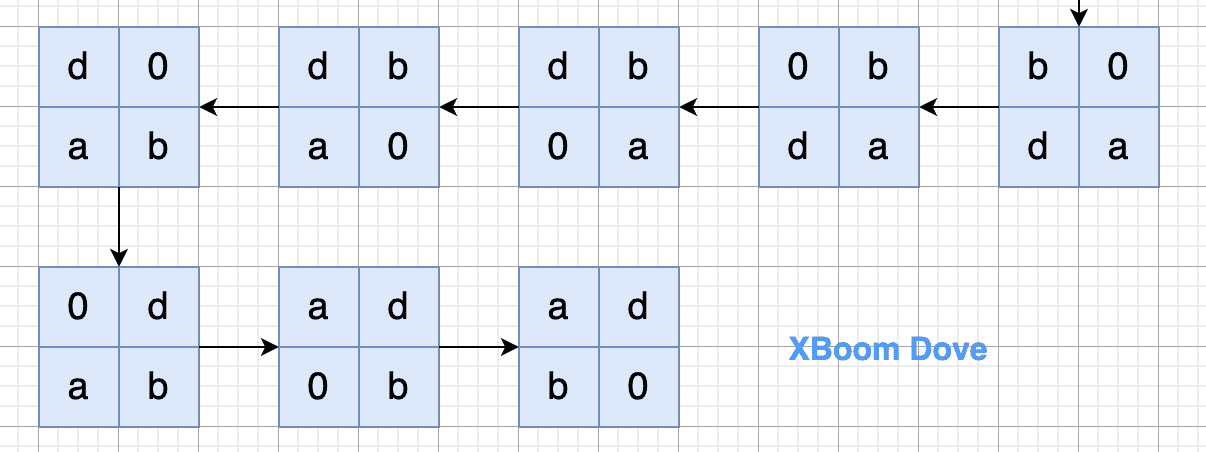
接着考虑在一个标准格式中,在两个具有相同边的区域交换数据,由于标准格式的对称性,所以只考虑上半部分
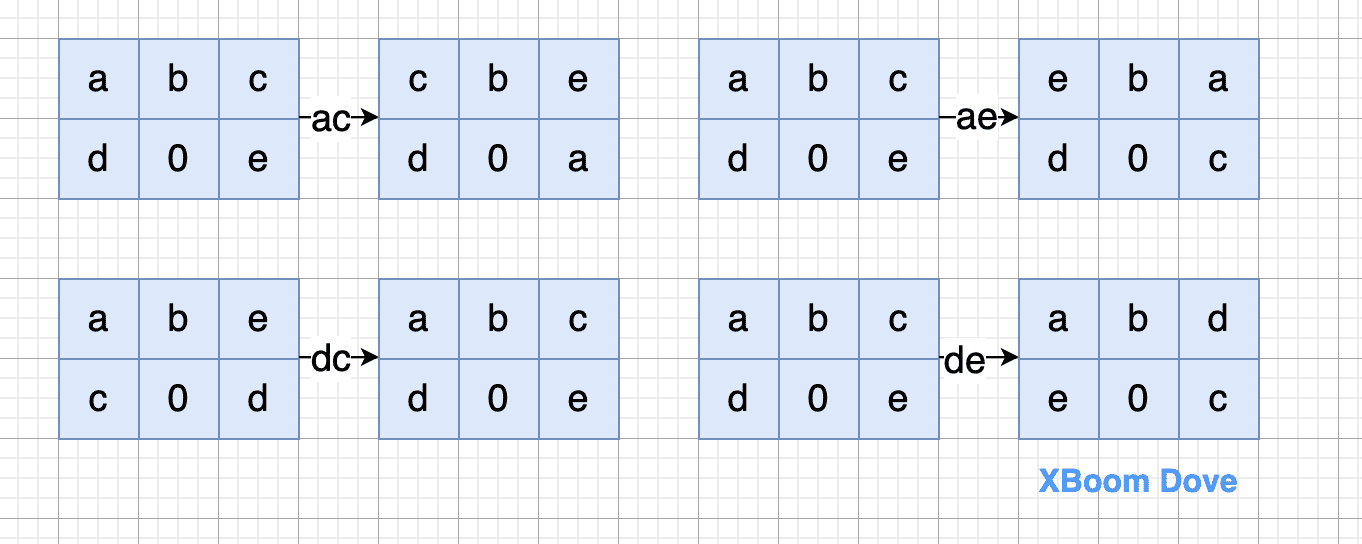
这个图形转换根据上述原则手动绘制交换流程更容易理解
得出的规律1: m 属于 {a ,d},n 属于 {c, e},p 属于 {a, d} 但 p != m,q 属于 {c, e}但 q != n,那么交换 m n,则 n 来到 m 之前的位置,而 m 来到 q 之前的位置,q 来到 n 之前的位置
得出的规律2:abc 可以经过转换编程 cab 或者 bac,不影响其他行且逆序对不变

对于标准格式,如果它们的逆序对的奇偶性相同,那么它们是等价的
证明:
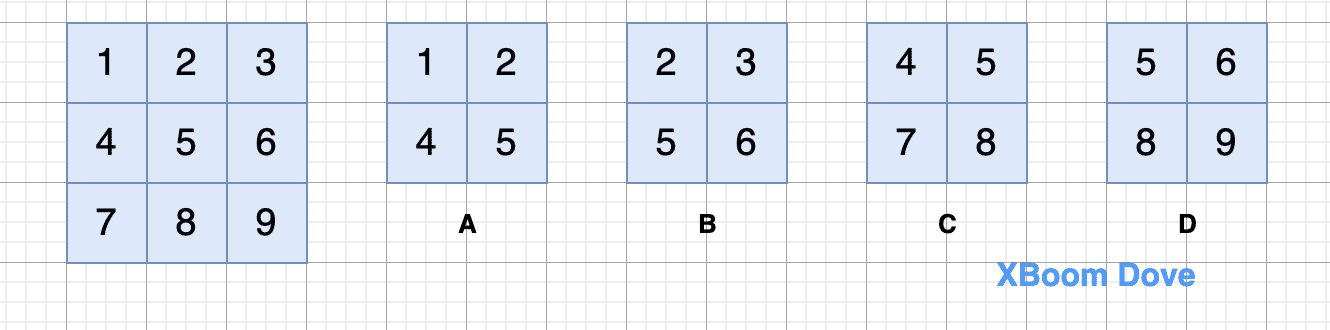
首先,将九宫格分为A、B、C、D分为四个区域
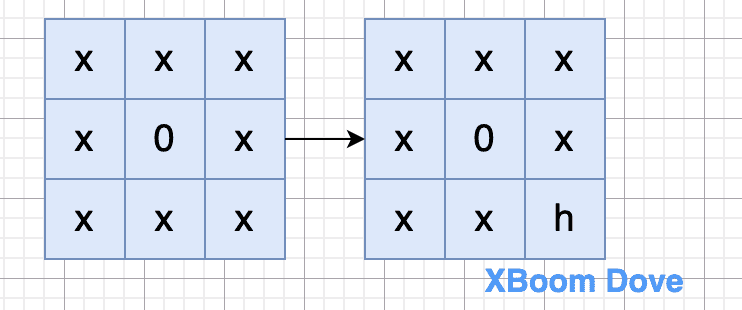
第一步,将 h 移动到位置 位置 9,这是肯定可以的
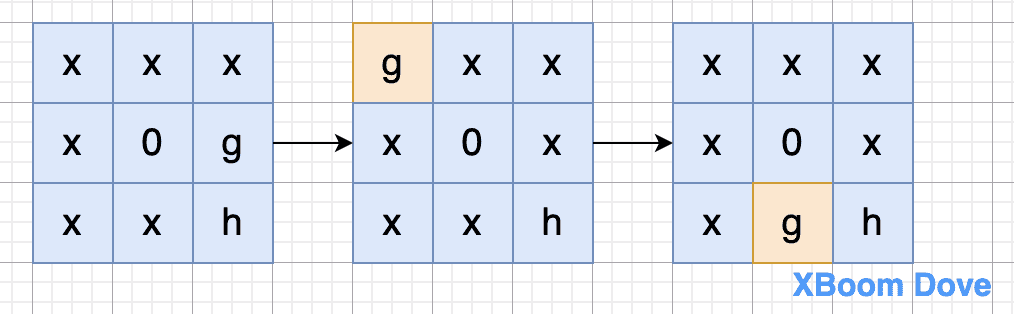
第二步,将 g、e 移动到区域D
为什么不考虑g、e的顺序,因为可以在不影响h的情况下 g 在 位置 6 与 位置8 任意切换
-
2.1 如果 g、e 已经在区域D,那么不需要移动
-
2.2 如果其中 g 在 区域D,而e 在其他区域
-
2.2.1 e 在区域A
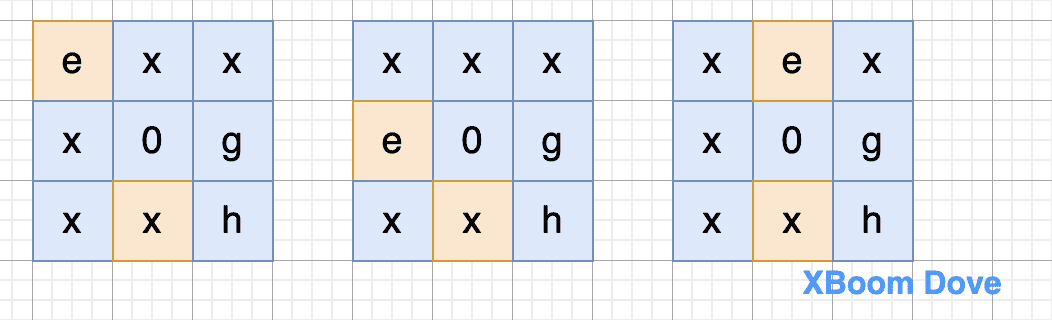
-
2.2.2 e 在区域B
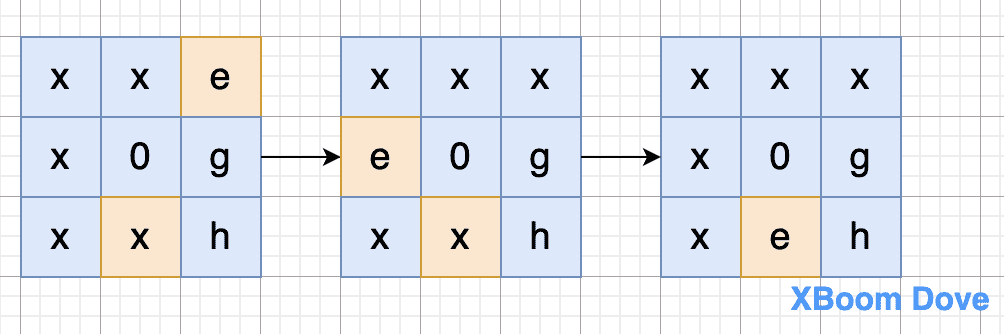
-
2.2.3 e 在区域C
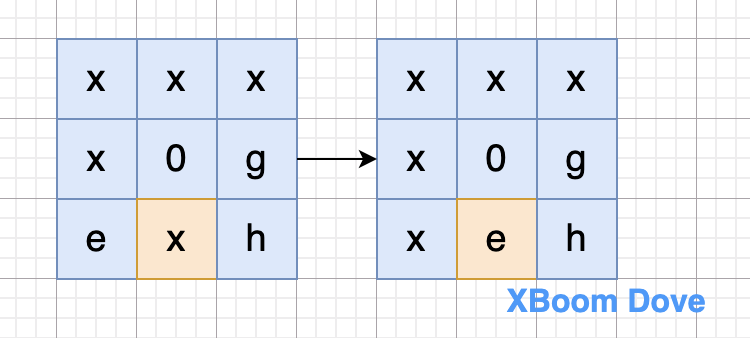
第三步,将 b、c 移动到 B区域
-
3.1 如果 b、c 都在区域 B,那么不需要移动
-
3.2 如果 b、c 有一个在区域B,那么
b 、c 的位置也同样可以忽略,如果b、c是正常顺序,那么也可以在不影响 g e h 位置的情况下调整 b c 的顺序
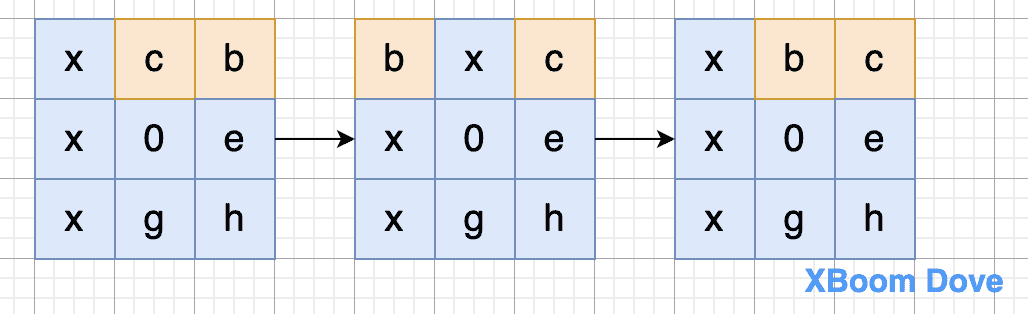
-
3.1.1 如果在位置3
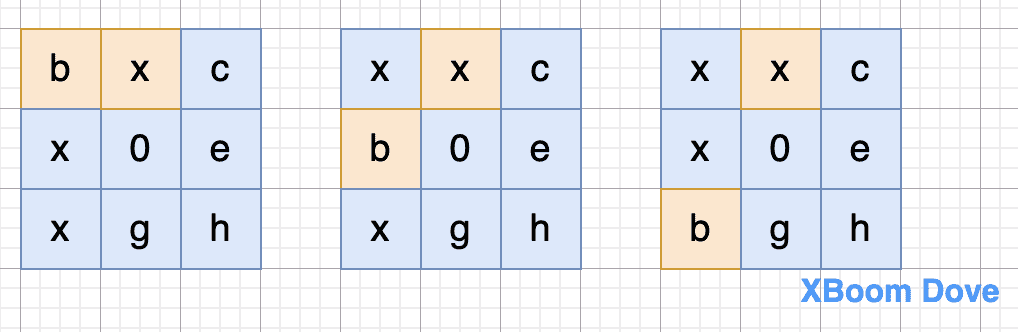
-
3.1.2 如果在位置2,那么先将c移动位置3再执行上述步骤
-
-
如果 b、c 都不在区域B,同理将c 移动到位置3,然后在执行上述3.1.1 步骤
-
第四步,在不影响bcehg的情况下调整adf的顺序
- 规律二在 此场景下仍然适用,所以首先将防止到位置7
- 根据定理1,如果两者等价,那么它们的逆序对是相同的。而如果位置1与位置3交换其他位置不变,那边整个序列的逆序对是变化的。所以a一定在位置1,d在位置4
所以,如果奇偶性相同,那么两个状态都能转换成一个相同的标准状态,那么两个状态之间是可达的
得出结论:两个排列的逆序对奇偶性相同,那么在八数码中必可达
参考链接
- https://blog.csdn.net/u011008379/article/details/40144147
- https://chengfeng96.com/blog/2018/05/26/利用BFS,DFS,A-解决八数码难题/
- http://www.huaying1988.com/blogs/8_Puzzle_StrictProof_SolutionAlgorithm_AndOthers/detail.html
- 《A constructive proof for the subsets completeness of 8-Puzzle state space》