堆(Heap)是具有以下性质的完全二叉树
-
每个结点的值都大于或等于其左右孩子结点的值,称为大顶堆
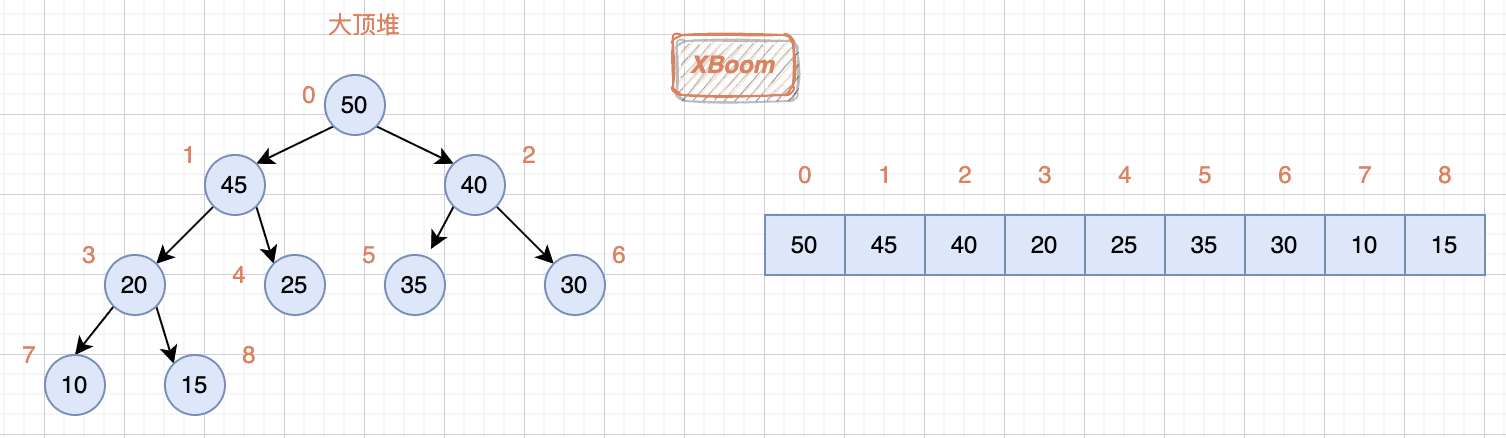
-
每个结点的值都小于或等于其左右孩子结点的值,称为小顶堆
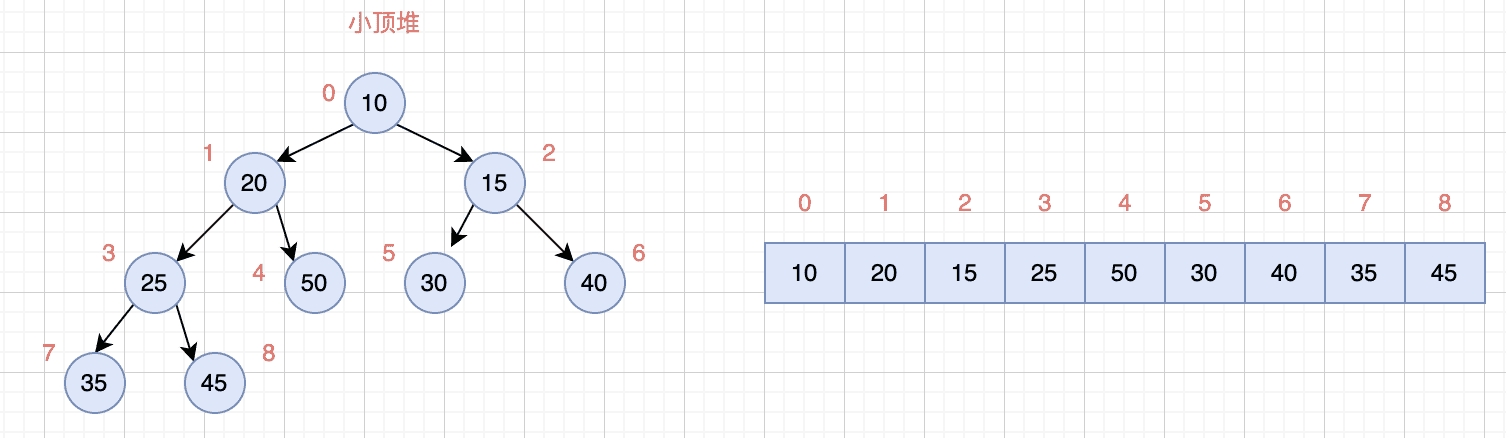
完全二叉树:除了最后一层,其他层的节点个数都是满的,最后一层的节点都靠左排列
**问题 **:那左右子节点有谁大谁小?没有要求!!!
大根堆,每个子结点都要小于父结点,不区分左右儿子谁大谁小,也不必保证某个 孙子结点 一定要小于另一个 儿子结点
小根堆,每个子结点都要大于父结点,不区分左右儿子谁大谁小,**也不必保证某个 孙子结点 一定要大于另一个 儿子结点 **
也就是说,即使组成了 大小根堆,它们的排列还不是有序的,只是保证
大顶堆:arr[i] >= arr[2i+1] && arr[i] >= arr[2i+2]
小顶堆:arr[i] <= arr[2i+1] && arr[i] <= arr[2i+2]
实现原理
首先明白两个概念:向下调整 与 向上调整
向下调整:指的是为了满足堆的性质而向下不断比较调整父子节点的关系,一般用于堆删除一个元素
- 从堆的根节点开始(通常是数组的第一个元素),比较当前节点与其子节点的值。
- 如果当前节点的值小于其子节点中的一个或多个节点的值,那么将当前节点与最大的子节点进行交换,以满足大顶堆的性质。
- 重复上述步骤,直到节点没有子节点或者节点的值大于等于其子节点的值
这里删除堆顶元素之后还向下调整的原因是,会将最后一个元素放置到堆顶
向上调整:指的是为了满足堆的性质而向上不断比较调整父子节点的关系,一般用于堆插入一个元素
- 在堆的最后一个位置(通常是数组的最后一个元素)插入新元素。
- 比较新插入的元素与其父节点的值。
- 如果新元素的值大于其父节点的值(对于大顶堆),则交换新元素与父节点,以满足堆性质。
- 重复上述步骤,直到新元素的值小于等于其父节点的值或者新元素已经成为根节点
实际应用中还有一种情况,比如需要从堆中直接删除一个元素(元素已经失效,需要释放该元素重新调整小根堆的结构),此时会出现一个空洞
- 将最后一个元素 last 放到被删除的位置
- 如果删除位置不是堆顶元素,且父节点大于 last 。那么根据小根堆的性质,last 应该从这个位置开始向上调整
- 如果删除位置是堆顶元素或者父节点小于last。那么根据小根堆的性质,last应该在删除位置的下发(或不变)
所以上面其实就是堆的插入和删除过程了,原理就是只在头尾处理,然后进行向上或者向下调整,保证大根堆、小根堆的性质
问题 1:为什么不在删除对顶元素之后,直接将第二大元素放到堆顶呢?
答:这样的后出现空洞的情况,就需要进一步处理

所以,这里改变思路:将最后一个节点与堆顶交换,然后删除最后一个元素,最后利用同样的父子节点对比方法。对于不满足父子节点大小关系的,互换两个节点,并且重复进行这个过程,直到父子节点之间满足大小关系为止。这就是从上往下的堆化方法

问题 2:知道了插入和删除,它首要条件是有一个堆,所以堆从哪里来
答:方案有两种
- 从前往后,尽管数组中包含 n 个数据,假设起初堆中只包含一个数据,就是下标为 0 的数据。然后不断的插入将下标从 1 到 n - 1 的数据依次插入到堆中。每插入一个元素都向上调整到合适位置
- 从后往前,依次与子节点进行比较,因为叶子节点无法与子节点比较,所以就需要从最后一个非叶子节点比较。每次都向下调整到合适的位置
问题 3:最后一个非叶子节点如何表示
答:假设最后一个非叶子节点下表是 i (i 从 0 开始)
- 如果它的左子节点是最后一个节点,那么最后一个节点下标就是
2i + 1。整个二叉树的长度就是len = 2i + 2 - 如果他的右子节点是最后一个节点,那么最后一个节点下标就是
2i + 2。整个二叉树的长度就是len = 2i + 3 - 所以最后一个非叶子节点的下标就是
i = len / 2 - 1
问题 4:建堆的过程有两种,哪种更好
答:第二种方式可以节省一半的时间
- 第一种方式需要对
n-1个节点进行堆化,每个节点堆化的时间复杂度为O(logn),所以它精确的时间复杂度为(n-1)*O(logn) - 第二种方式从非叶子节点开始,需要对
n/2个节点进行堆化,精确的时间复杂度为(n/2)*O(logn)
问题 5:既然不关心左右节点大小,那样怎么样做到整个有序呢?
答:就像删除堆顶元素一样。当堆顶元素移除之后,把下标为 n 的元素放到堆顶,然后向下调整,让剩下的 n−1 个元素重新构建成堆。堆化完成之后,再取堆顶的元素,放到下标是 n−1 的位置,一直重复这个过程,直到最后堆中只剩下标为 1 的一个元素,排序工作就完成了。

一个包含 n 个节点的完全二叉树,树的高度不会超过 log2n,堆化的过程是顺着节点所在路径比较交换的,所以堆化的时间复杂度跟树的高度成正比,也就是 O(logn)。
插入数据和删除堆顶元素的主要逻辑就是堆化,所以,往堆中插入一个元素和删除堆顶元素的时间复杂度都是 O(logn)
因为每个元素都需要进行删除的过程,所以堆排序整体的时间复杂度为 O(nlogn)
代码实现
1 |
|
堆排序应用
-
Top K问题
从堆的定义来说,很容易想到堆顶元素是TOP 1,那么如何求经典的TOP K问题?
如果求最大的Top K 元素,是建立大顶堆,还是小顶堆
- 如果用大顶堆,堆顶是最大的元素,新加入的元素必须和所有的堆中元素做比对,显然不够划算;
- 如果用小顶堆,那堆顶元素是最小的元素,新加入的元素只要和堆顶元素做对比,如果比堆顶元素大,就可以把堆顶的元素删除,将新加入的元素加入到堆中
每次求TopK的问题的时候,只需要直接返回堆中所有元素即可,每次堆化的算法复杂度为O(logK),那么N个元素堆化的时间为O(nlogK),如果不用堆,每次新增元素都要重新排序,再取前面N个
-
定时器应用
独立线程,以超时时间建立了一个小顶堆,如果堆顶元素为2分钟,清理连接的线程的休眠时间设置为2分钟,2分钟后取堆顶元素,执行连接关闭操作。
-
求中位数和99%的响应时间
动态数组取中位数:
- 如果n为偶数,前n/2数据存储在大顶堆中,n/2存储小顶堆中,则大顶堆的堆顶元素为要找的中位数
- 如果n为奇数,可以将前n/2+1个数据存储在大顶堆中,后n/2存储在小顶堆中
如果添加新数据,则将数据与大顶堆中的堆顶元素比较
- 如果小于等于大顶堆中的元素,就插入到大顶堆中
- 如果比大顶堆的堆顶大,那就插入到小顶堆中
- 如果插入数据后不满足要求两个堆的数量为n/2和n/2 或n/2 和n+1/2 的要求,需要调整两个堆的大小,从大顶堆中删除堆顶元素,或小顶堆中删除堆顶元素,移动到另外一个堆中即可。
99%的响应时间:如果一个接口的有100个访问请求,分别耗时1ms,2ms,3ms…100ms,那么按照访问时间从小到大排列,排在第99位的访问时间,就是99%的访问时间,我们维护两个堆,大顶堆的元素个数为n * 99%,小顶堆的元素个数为n*1%,那么大顶堆中的堆顶元素即是所求的99%的响应时间,和中位数的应用一样,只是中位数中的应用更特殊一点
-
优先级队列
优先级队列和通常的栈和队列一样,只不过里面的每一个元素都有一个"优先级”,在处理的时候,首先处理优先级最高的。如果两个元素具有相同的优先级,则按照他们插入到队列中的先后顺序处理